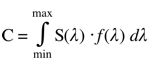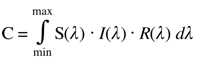摘要：最近对“颜色”产生了一点好奇，于是阅读了几篇文章，这里记录一下。这里只记录个人认识，本人非科班出身，此篇纯属个人参考，故不做过深思考。本篇读完后可以带着疑问去读关于颜色的一点认识（二），那篇是对本篇的补充。

颜色

人类都是视觉动物！我们每天都在谈论颜色！

“你的衣服颜色真漂亮,在哪里买的?”
“我觉得还是绿色更保护眼睛”
“你的显示器好暗”
“这个灯泡是不是有点太黄了?”

玄学警报

我们在看很多照片的时候，会产生一种 德味儿、大师、毒! 的感觉。这种感觉我们统称为“玄学”。
这个系列中，我们尽可能的避免这种关于玄学的争论，将重点放在色彩科学本身上。
对于颜色是否“好看”、是否“优雅” ，请将所有的这些都归为 脑内PS ，因为最强的影响还是来自于我们自己的大脑和以往生活的认知。

色彩的旅程

到底我们是如何感觉到颜色的呢？

我们用一个简单的图示来表示颜色从出生到结束的整个旅程。

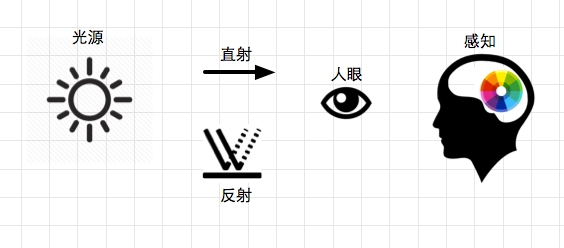
首先，需要一个光源。

光源发射出许许多多的光线。这些光线有些直接射入我们的眼镜（直射），有些会撞到某些物体(反射)，然后再反射到我们的眼睛。

然后，当人眼接收到这些光线后，眼底的各种细胞产生了一系列精密的化学反应。

由此产生的化学信号通过神经传递到我们的大脑。

最终在我们的大脑内形成了对于颜色的感知。

光源

光源，Light Source，就是产生光的物体，也是色彩科学的开始。

简单来说，如果没有光，你是不可能在黑暗之中看出“色彩” 的。

光本身其实就是一种纯粹的物理现象，在光达到你的眼睛之前，它其实是没有“颜色” 的。这个时候光所拥有的属性仅仅是 波长(wavelength) 和 能量分布 。

波长(wavelength)

光是一种电磁波，一般来说人眼可见的光的波长在 380nm~780nm 之间。可以认为单一波长的光辐射就表现为一种颜色（比如），即所谓的单色光。

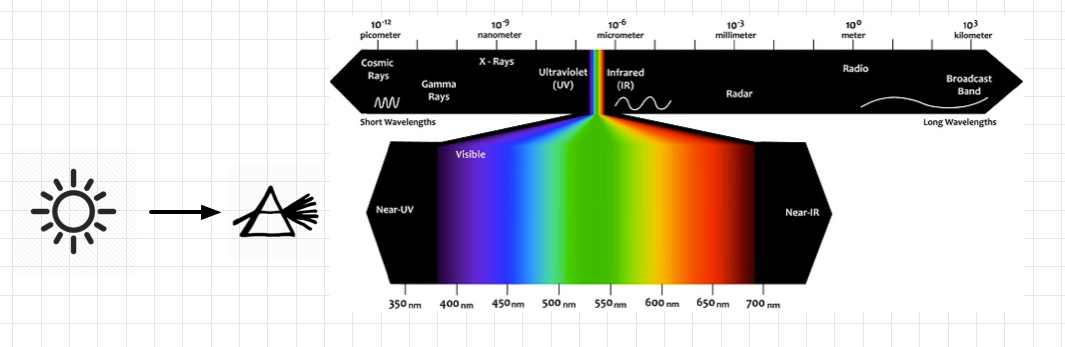
我们小时候都玩过把一个三角形的棱镜放到太阳光下面，然后光线透过棱镜之后，就会出现彩虹的条纹。

这其实就是利用棱镜将不同波长的光线区分开。

正常人类可以看到的波长范围是 380nm ~ 780nm ，这个范围内的光线叫做可见光。

超过这个范围的光线叫做 红外线 和 紫外线（当然，还有很多其他的光线）。

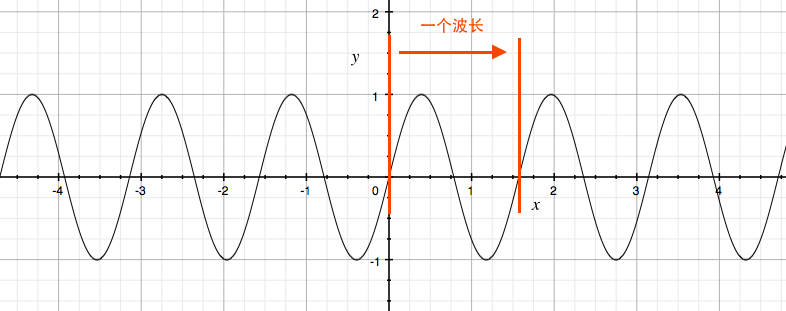
光线在宏观的尺度上表现的特性 波 。

简单来说，你可以想象成湖面上泛起的波纹。

波长，就是指一个波的的长度，光线的波长单位一般是nm(纳米)。

波长越短，人眼感知的颜色就会越靠近紫色；反之波长越长，人眼感知的颜色就会约靠近红色。

其中 555nm 的波长就是我们说的绿色。

光谱

说到这里，我再一次希望大家先忘掉“颜色”，只考虑光线其实就是不同波长的波纹。

就好像是你在湖里丢了一块石头，然后激起了某个波长的波纹；

然后你又丢进去第二块石头，产生了另外一个波长的波纹......

然后很多不同波长的波纹叠加在一起，就形成了最终的波形。

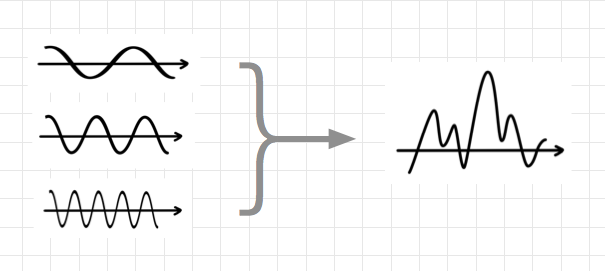
从上面的图中，可以认为是三种不同波长的波纹，叠加在一起，形成了最终的波形。

三合一，这个很简单，哪怕是有100种不同的波纹，也不过就是都加在一起，反正最后都会形成最终的某种样子。

现在问题来了，如果我直接给你一个最终的波纹形状，让你将它拆解成各种波长的组合......

天啊，反过来就非常难了！就好像让你计算 12 x 15 x 13，你总是可以计算出最后的结果，但是如果直接让你将2340拆解成三个整数的乘积......就非常难了。

别怕，人类还是非常聪明的！他们发明了一种叫做分光光度计的东西，能够完成这种波长的拆解工作，并且告诉你每种波长的光线的具体能量强度。

分光光度计的原理

分光光度计的原理，可以大体认为是有个棱镜，这个棱镜利用光学的物理特性，将不同波长的光线分开!然后在每种特定波长的位置，放一个探头，这个探头只会对这种波长的光线产生感应反应。

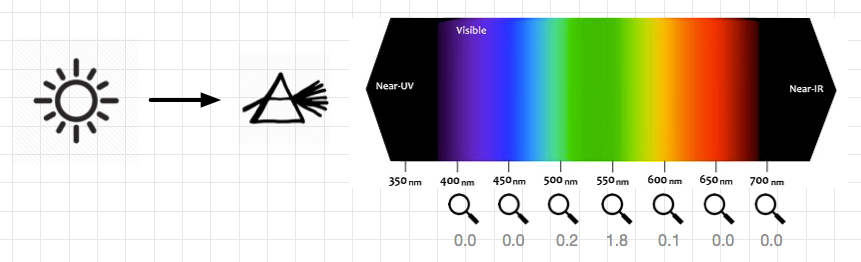
例子中假设有7个探头，分别对400、450、500...... 700nm 的波长进行测量，当然你也可以放很多的探头，甚至 1nm 就放一个。

每个探头接收的就是这种波长的能量：可以理解成单位时间内，有多少个这种波长的光子打到探头上。

最后将每个探头的读数写出来，这就是这种光谱能量分布！

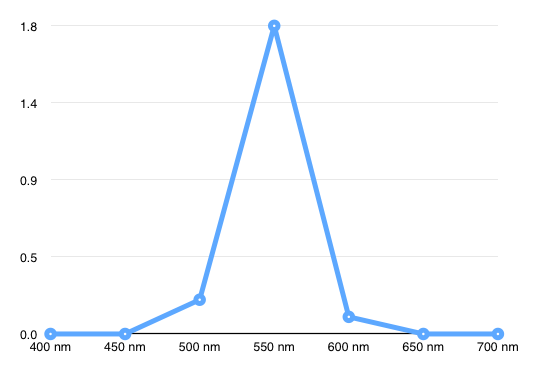
这个例子中的光线能量都集中在550nm 附近,所以认为这是个绿色的光线。

有了分光光度计，你就完成了两件非常重要的事情，也可以说是整个色彩科学的第一步：

• 将一种混合波长的光线，拆分成为各种单一波长光线的组合
• 能够测量每种单一波长光线的实际能量

有了它，我们终于可以不用按照语言、感受、猜测、对比来描述光线，而是通过每种光线中有多少种不同波长的光、每种波长的光的能量分别是多少来进行描述。

这样就脱离了任何主观的评判，形成了完全的客观、定量的描述，为后面所有的色彩科学奠定了基础。

下面是一些光源的光谱能量分布：

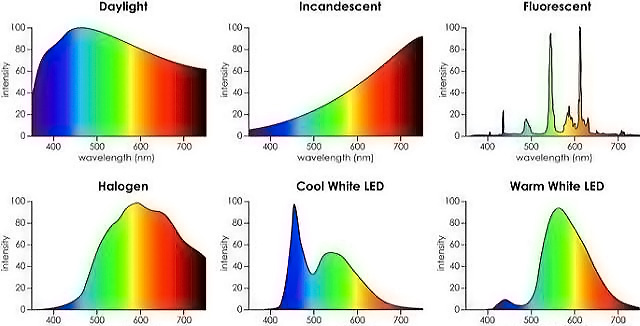
光强度

关于光的强度有两种定义：一种是物理上的强度 辐射能通量 (radiant flux 单位：W 比如：20W的绿色灯泡和20W的红色灯泡，能量是一样的）另外有一种是人眼感观上的强度 光通量（Luminous Flux 单位：lm 比如：20lm的黄绿光和20lm的红光一样亮）：

• （1）辐射能通量（radiant flux）
  辐射能通量是Radiometry（辐射度量学）上的概念，是物理上的强度，反映实际的能量，单位是瓦特（w）。

• （2）光通量（Luminous Flux）
  光通量是Photometry（光度学）上的概念，按照人类眼睛对不同波长光的敏感程度制定的物理量，单位是流明（lm），反映了一个光源的发光总量。

  

  举个例子：

  对于一个光源，如果其功率很高，但是发出的光都集中在人眼不敏感的红外波段，那么从辐射度量学（radiometry）上面，这个光源很强，但是从光度学（photometry）方面，这个光源就比较弱。所以人眼对于光谱中不同波长的响应就是两类参数之间转换的关键了。这个值叫 Luminous efficiency（Φ(λ)）。因为 555nm黄绿光 处人眼最灵敏，所以用这个波长的数据作为相对数值的标准，也就是 Φ(555nm)=1 ；其他波长的Luminous efficiency（Φ(λ)）则都是一个小于1的相对值。对应的数值见下右图，曲线见下左图：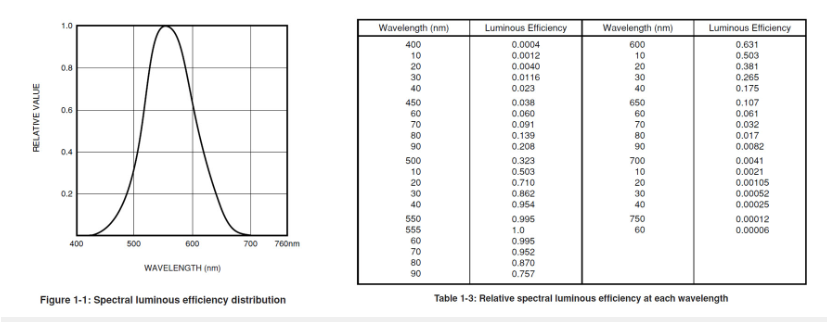

  

  在人眼最灵敏的555nm黄绿光处，流明(lm)和瓦特（W）的换算关系常数 Km = 638 lm/W 。或者说，功率为1w的555nm黄绿光，其光通量为638流明。而对于其他波长的光，由于人眼不那么灵敏，同样功率为1W的光，其光通量是达不到638lm的；或者说同样1W的光，我们会觉得其他颜色的光不及555nm的亮，luminous efficiency（Φ（λ））越小，我们会觉得这光越弱。

  由此我们可以得出638 lm的555nm的黄绿光和638 lm的620n的红光 所需要的功率分别为1w 、2.62W。

• （3）光强度（Luminous intensity）

  • 坎德拉（cd）

    坎德拉（cd）被用于描述在人眼看来，一个光源在某个方向亮不亮。类比压力和压强的概念，光通量就是压力，光强度就是压强。

    以下是坎德拉的物理定义：

    给定一个频率为 555 nm的点光源（黄绿色可见光），该辐射源向四周发光。
    如果该光源在一个球面度内的功率为1/683 瓦，则该光源在该球面度的光强度为1cd。

    由此也可推导出 假如一个频率为555 nm，发光强度为1 cd的点光源，向四周均匀发光，则该点光源的光通量为4π lm，所需要的功率为4π/683 瓦。

  • 尼特（nit）

    尼特（nit）是衡量亮度的单位，nit = 坎德拉每平方米（cd/m2）。其中的坎德拉是衡量发光强度的单位，平方米则是衡量面积的单位。Nit，来源于拉丁语的“nitere”，意为照射。

• （4）照明度（llluminance）
  照明度主要用来反映被光源照射物体的明亮程度。可以通过照明度来衡量人眼所能感受到的光的明亮程度了。比如办公室中的照明应该为320 lux到500 lux。

  照明度（I）= 每单位面积每秒所接受的光通量 = P / A
  其中，
  I：光照强度，单位：lux；
  P：入射光束的光通量，单位：lm；
  A：照射面积，单位：m²。
  

总结一下：光通量反映了光源能发出多少光，类比压力。光强度反映了光源在某个方向亮不亮，类比压强。照明度主要反映被光源照射物体的亮不亮。

光谱能量分布（spectral power distributions (SPD)）

一般光源发出的光是由许多不同波长的辐射组成的复色光，且各个波长的辐射功率也不同。光源的光谱辐射能通量（能量）按波长的分布称为光谱功率（能量）分布（spectral power distribution）。

光源的光谱功率分布可用曲线表示。

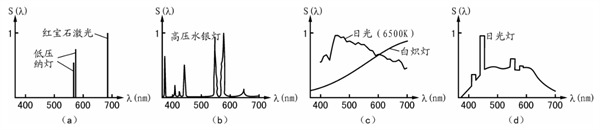
绝对功率分布曲线：以波长为横坐标而以光源辐射的各种波长光能量绝对值为纵坐标所作的曲线。
相对光谱功率分布曲线：如令光谱分布能量的最大值为“1”或其他数值，将光源辐射光谱的其他各种波长的能量与之进行比较，作归一化处理后，使辐射功率仅在规定的范围内变化，这样的光谱曲线就称为相对光谱功率分布曲线。每种光源都有独有的相对光谱功率分布曲线。光源的光谱相对辐射能通量功率分布决定了光源的颜色特性。

如果还不太理解光谱能量分布是什么可以参考：光源基础知识：光源的光谱功率分布曲线

光线的传播

光源产生了光线，然后光线在到达人眼之前会历经千辛万苦。

有的光线运气比较好，直接就到达了人眼，我们称之为直射光。

有的光线运气不好，会撞到其他的物体，然后反射的光线再进入人眼，我们称之为反射光。

有的光线会穿过某些半透明的物体，然后到达人眼，我们称之为透射光。

还有一部分光线运气太差了，在撞到了物体之后，还会继续撞到别的物体......

直射光比较容易理解，相当于光源的能量分布原封不动的传递到了人眼。（我们不考虑介质产生的影响）。

反射光和透射光就比较特殊了，光线每经过一次反射或者投射，都会对光线的 光谱能量分布 产生一些影响。

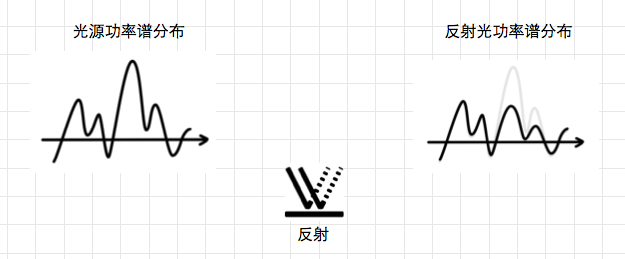
从图中可以看出来，光源原始的功率谱分布是某种样子的，但是经过反射之后的功率谱分布发生了一些变化。

仔细看看浅色表示的部分，就是缺失的部分，这种缺失正好就是反射造成的。

缺失的部分可以理解成:
在500nm 和 600nm 波长附近的光线的能量变弱了。

是什么造成了这些光线能量变弱了？

没错，就是反射！反射物体吸收了这部分光的能量。

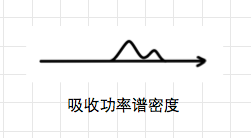
将功率谱分布进行差异比较，得到的差异部分就是反射物体的吸收功率谱分布。也就是这个物体对于入射光线能量的影响。

可以看出这个物体对于 500nm 和 600nm 附近的光线有能量的吸收，也就说这个物体可能会比较多的吸收绿色和黄色的光线。

自然界中物体之所以能够呈现不同的颜色其根本原因就在于物体对光具有选择吸收和反射的性质，也就是说物体本身的光谱特性是物体呈现不同颜色的主要原因。一般来说，透明物体的颜色取决于其透射光的光谱，而非透明物体的颜色取决于其反射光的光谱。

人眼的特性

人眼是生物学上的杰作。一方面它非常的精巧，另一方面它又有一些明显的缺陷。

但是不管怎样，我们的眼睛现在就是这样，证明它已经足够满足现在人类生存需求。

如果要是展开来说人眼，那么多少篇幅都是不够用的，涉及到了解剖、生物、神经...... 太多的专业知识。

这里只是大体的来说明一些和色彩科学密不可分的特性。

可变分辨力

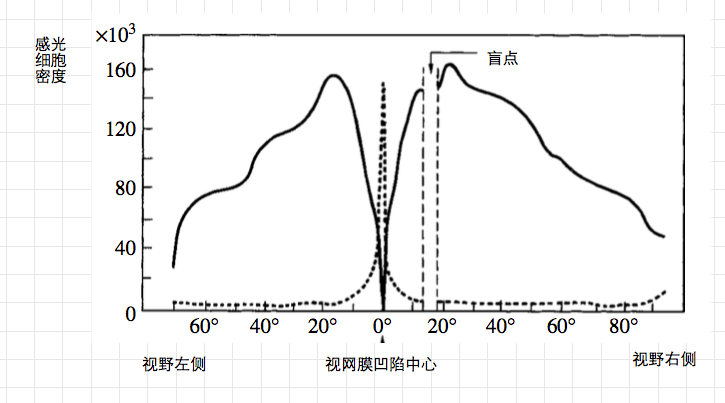
和数字设备不同，人眼的分辨力其实分区域的。

数字摄影机的最大分辨力是由CCD 上感光原件之间的最小距离决定的。两个感光原件的距离越小，分辨力就越强。

人眼的分辨力是由视网膜上的细胞来决定的，如果两个感光细胞离的越近，那么分辨力就越强。不幸的是，感光细胞只有在视网膜黄斑的附近才会特别的密集，离黄斑越远，感光细胞的密度就越小。

这就造成了你真正能够看清东西的角度，其实也就是不到10°，不信你试试，你很难用余光来读文章！但是你依旧可以通过余光来感受光亮和物体的移动。

相对亮度感知

这个现象可以很简单的通过例子说明。

人眼对于亮度的感知不是绝对的，也不是线性的。

比方说，在完全黑暗的环境中，点亮一个灯泡。这时候你可能觉得是“这么亮”。然后同时点亮1000个这样的灯泡，你可能只是觉得10倍的“这么亮”。

再换个例子，我拿个很亮的探照灯晃你的眼睛，你可能觉得已经亮的睁不开眼了。但是让你看太阳，你也是觉得亮的睁不开眼。这个光源都是“非常亮”！但是其实两个光源的能量可能相差1000倍。

人眼的适应性

很多人说人眼是HDR 的，因为人眼既可以分辨出高光中云彩的不同层次，还可以分辨出阴影里面不同物体的区别。

这句话，其实丢掉了一个很重要的条件，那就是同时！

人眼的确可以区分高亮的细节，也可以区分暗部的细节，但是不能同时达到这两个条件...... 比如说你看着阳光明媚的天空的时候，其实不能分辨出楼道阴影里面的人。

奇怪的事情就在这个时候发生了，当你努力注视楼道的阴影一段时间后，你发现你就能够看清阴影中的不同物体了，这就是人眼的适应性。随着时间的推移，你发现你越来越可以清晰的分辨出阴影中的物体了。

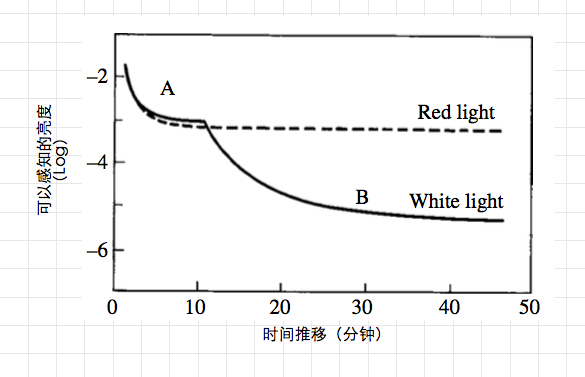
你刚刚进入进入黑暗环境的时候，可以感知到10^-2 cd/㎡的亮度,但是随着时间的推移，10分钟之后你就可以感觉出10^-3 cd/㎡。然后随着时间继续的推移，50分钟过后你甚至可以分辨出10^-5 cd/㎡的亮度！相当于在50分钟内，你看到了刚开始时候千分之一的亮度。

人眼接受光线

前面说到的人眼特性，对于色彩科学来说都是一件不好的事情。为什么？因为太不确定了！你想想，我们好不容易可以完全客观的测量出光线的“数值”，结果人眼又会变来变去，分辨力会变、亮度的感知也不是绝对线性的、甚至能力还会随着时间而变化...... 这就是完全无法客观描述的节奏啊！

但是人类还真是聪明，又想出一些办法来研究人眼到底有哪些可以客观量化的特性。

感光细胞

人眼可以感受到光，但是为什么其他地方不行呢？因为视网膜上面有感光细胞。感光细胞大体分为两种，一种是杆状细胞，主要负责感知亮度；另外一种是椎状细胞，主要负责感知色彩。

杆状细胞对于光非常敏感，基本上只要有5~14个光子打到杆状细胞的话，就会开始产生神经信号。

而椎状细胞需要100~1000个光子的能量才会开始产生神经信号。

这样就可以解释为什么光线很暗的时候，你很难看清“颜色”。

你知道么?
椎状细胞基本都分布在黄斑附近，距离越远，分布的就越少。
而杆状细胞在视网膜上基本是平均分布的。
这就是为什么视觉中心的分辨力高，而视野的外围只能感知亮度。

椎状细胞其实还分为三种椎状细胞，我们把他们叫做L细胞、M细胞、S细胞。视网膜解剖结构中各个细胞的占比如下：63% L视锥细胞、31% M视锥细胞和6% S视锥细胞。（有可靠的证据表明，这些比例因人而异。）

下面这个图片表现每种细胞对不同波长的光作出响应比例。为了方便观察，作了归一化处理。

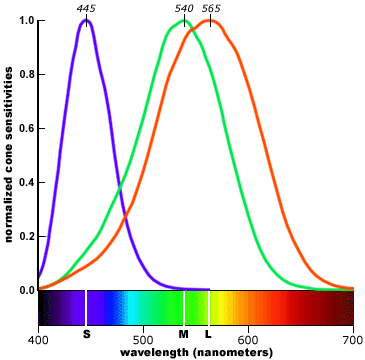
详细的说明就是：

• S细胞负责感受 445 nm 附近短波长的光线。当波长为445 nm的光照射，6%S视锥细胞中100%作出了响应（图中坐标为 445,1 ）。当波长为425 nm的光照射，6%S视锥细胞中只有50%的比例作出了响应（图中坐标为 425,0.5 ）。
• M细胞负责感受 540 nm 附近中波长的光线；
• L细胞负责感受 565 nm 附近长波长的光线。

人眼的本质

人眼可以认为就是一个接收器。它的作用就是将外界的光线的输入，转化成为输出神经电信号。

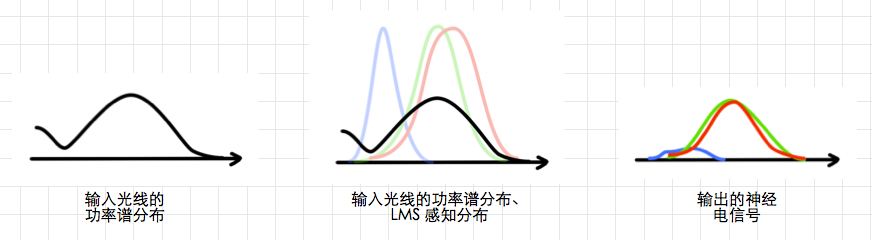
输入光线的功率谱分布，照射到眼睛，眼底的LMS感光细胞分别感应自己对应波长区域的能量。LMS 感光细胞根据接收到的总能量，传出对应强度的生物电信号。

如果写成数学的公式

C 表示输出的神经电信号
S(λ) 表示LMS 三种感光细胞的感知分布
f(λ) 表示进入眼睛的光线。

计算的方式叫做积分，你可能觉得有点陌生，没关系。用人话来说就是：输出的电信号的数值，就是曲线所覆盖的面积。

如果我们在稍微往前回忆一下，光线在入射到眼睛之前，还经过了反射的影响.

那么完整的公式应该怎么写呢：

I(λ) 表示光源的功率谱分布，R(λ) 表示反射物体的吸收功率谱分布。二者相乘，正好就是f(λ)。
也就是之前说的，进入人眼的光线等于受到反射物体影响后的光源光线。

色盲的原理
色盲的原理其实就是由于某些原因导致LMS感光细胞的感知分布和正常人不太一样。
这样相同的光线对于色盲患者来说，产生的神经电信号就会和一般人不同，进而导致之后大脑对于色彩的感知出现不同。
比方说，红绿色盲，可能是M、L 两种感光细胞的感知分布曲线非常接近。这样不论输入的光线是红色还是绿色，M、L 两种感光细胞产生的神经电信号也是非常接近。这样就导致大脑无法区分两种颜色，因为他们的信号是一样的......

大脑的感知

不管前面发生了多少事情，最后能够让你知道哪种颜色的还是你的大脑。但是不幸的事情又发生了，大脑也不是绝对理性的，很多奇怪的事情都会发生。

这些就很难有科学的解释了，大多都是现象，你问我为什么？我也不知道，但是他们都是的的确确存在的。

色彩记忆性

不知道你有没有过这样的感受，当你看到某个颜色之后，尝试记住它。过一段时间之后，我让你在很多相近的颜色中挑选刚才你看到的颜色。你想要根据记忆直接选择正确的颜色？这很难啊！人脑对于色彩的记忆性是很差的......

色彩的相对性

当你看到某种非常饱和的颜色后，尝试一直看着这个颜色，慢慢的，你就会觉得这个颜色变得没有之前那么饱和了。但是当你看到两个有对比的颜色时，哪怕这个颜色并没有之前的饱和，你还是会觉得这个颜色是非常饱和的。

如果你看到一个小的色块，你会觉得这个颜色没有一整面墙的颜色饱和。其实小色块和整面墙的颜色是一样的

色彩的适应性

如果你进入一个暖光灯环境，看到一张白纸，你会觉得纸张是暖黄色。但是慢慢的，你就会开始适应这种暖黄色。用不了多久，你就会发现纸张是白色的，而且你的大脑会根据这种新的白平衡来校准周围所有的色彩。但是一旦一离开这个环境，马上给你看同一张白纸,你就会觉得这个白纸是微微发蓝的冷色。

各种情绪、未知情况影响

你的心情也会影响到对于色彩的感知。就好像歌里唱到的:

我的人生是黑白的

色彩空间的历史

俗话说的好，想要了解一个事物，都要了解它的历史。很多当前的现象都是尤其长久的历史原因的。比方说为什么中国的用电是220V？为什么感冒了要刮痧？为什么小时候爸妈都是说你是捡来的……

如果想要了解为什么色彩空间会变成现在这个样子，就非常有必要聊聊有关历史，当读完了这本历史书之后，你可能就会明白一些为什么会有那么多的色彩空间、为什么色彩空间能够相互转换（可能吧……）

历史的车轮，谁也无法阻挡

科学的进步都不是一蹴而就的，往往中间会走不少的弯路，有的时候甚至会发现之前的结论完全是错误的。色彩科学的历程也是如此。但是一旦某个结论被公认是正确，那么之后的更多发现就会在此基础上帮助色彩科学的发展。

混沌的猜测年代【1800】

我们先飞到18XX 的年代，那个年代色彩科学的各种基础理论都是一片混沌。

总结一下：光通量反映了光源能发出多少光，类比压力。光强度反映了光源在某个方向亮不亮，类比压强。照明度主要反映被光源照射物体的亮不亮。

为什么？因为人们还没有搞懂一件最重要的事情：

人类感觉色彩的机制是什么？

于是乎，人类就开始了大胆的猜测。那个时候差不多有三种猜测：

• 猜测1：人们有100多种的感受色彩的细胞

  这种猜测的理由是，因为人们能够看到棱镜分光后的各种色彩。所以每种颜色对应一种感受色彩的细胞，于是就有100多种感色细胞。

  这种猜测现在看来真的是非常的简单粗暴，而且被时间证明是扯淡的。

• 人们有3种感色细胞，分别感受红、绿、蓝

  Thomas Young， 1802

  也就是俗称的三色理论。

  这种猜测有很多的事实根据的，因为当时人们发现色彩是可以通过三种基色进行混合的。而且神经科学也发现了视网膜上面的三种椎状细胞（LMS）。因此这套理论在当时迅速占据了主流。

总结一下：光通量反映了光源能发出多少光，类比压力。光强度反映了光源在某个方向亮不亮，类比压强。照明度主要反映被光源照射物体的亮不亮。

• 猜测3：人们有3种感色细胞，但是感受的是3对色彩

  Ewald Hering，1878

  和三色理论相同，这个理论也认为人类有三种感色细胞。但是三种细胞不是对应感受红、绿、蓝，而是感受三对色彩：

  黑——白
  红——绿
  黄——蓝

  这个理论也有直观的现象支持：比方说我们可以感觉到红里发黄 、绿里发黄、蓝里发红……但是从来没法感受到红里发绿、黄里发蓝。这就是补色的关系由来。

最后你猜怎么着，哪一个才是正确的？

猜测2 + 猜测3， 合在一起就形成了当下的色彩视觉模型

Munsell 色彩系统【1905】

在某些人们忙着搞清楚色彩感知原理的时候，另外一部分人也没闲着。
Albert Henry Munsell，美国艺术家，利用自己的艺术特长提出了Munsell 色彩系统。这个色彩系统后来被Committee of the Optical Society of America (OSA)在1930 年优化。

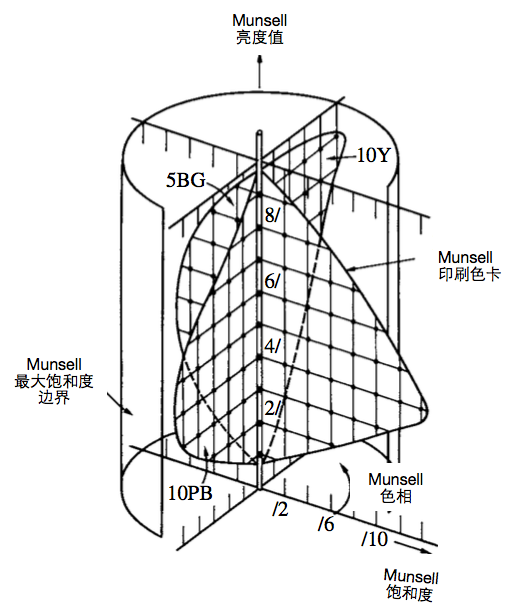
Munsell 通过很多色卡来描述色彩。

旋转的角度是 Munsell 色相
垂直的方向是 Munsell 的亮度值
从圆心向外的方向是 Munsell 饱和度

可以看得出来，Munsell 的确是艺术家，因为人们凭借主观感受来区分色彩的依据正好就是HSL。

这个系统里面没有过多的物理科学在其中，更多的是一种归纳和规范。但是Munsell 色彩系统也为量化描述色彩提供了一种方式。这是非常值得称赞的。

在这之前，人们交流色彩的时候可能是

“比苹果更红”
“鱼肚白”
“微微的清灰”

这些非常模糊的表述其实很难有统一的理解，当使用了Munsell 色彩系统后，一个颜色可以通过

H = 1.6YR
V = 6.3
C = 3.9

这种方式来表述，如果我们都有一个Munsell 色彩系统的标准色卡，那么就可以得到近似的颜色了。

CIE 1931 RGB Color Specification System 【1931】

虽然上面通过直观感受来量化描述的 Musell 色彩系统已经比文字描述好了很多，但是科学家们还是不满足，因为这不是最精确的“物理科学”级别的描述。我们需要一种完全客观的方式来描述色彩。

于是Commission Internationale de l’Eclairage （CIE）在1931年建立了一套色彩系统，希望能够完全客观的量化色彩。

此RGB 非彼RGB

很多人一看到RGB 就觉得这就是现在常说的那个RGB 色彩模型，一个立方体的盒子。

不不不！要说到你理解的那个RGB 还有好多年要走…… 这两个RGB 八杆子打不着。

观察者色彩匹配实验

不幸的是，在色彩科学中不存在“完全的客观”。因为最后总是需要人来看颜色，人就是主观的。
于是就需要想办法尽可能的弱化这部分主观可能导致的误差。CIE 的科学家想出了一个实验：

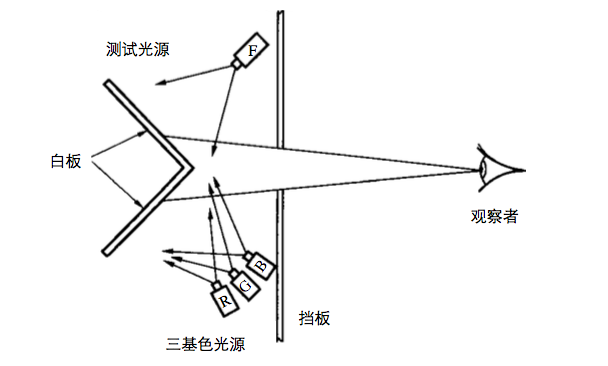
1. 观察者通过一个挡板上面的洞看到后面的两个白板；
2. 右边的白板被某个测试光源照亮，左边是被RGB 三个基色混合照亮。
3. 要求观察者，通过调整RGB 三个光源的强度，使得左右两边的颜色看起来一样。

4. 然后，记录下此时RGB 三基色分别的强度数值。如果用公式来表示：

   【测试光源】 ＝ R * [R] + G * [G] + B * [B]

   [R]、[G]、[B] 表示三个的基色，R、G、B 分别对应三种基色的强度。

   [R] = 光通量为 1 lm的700.0 nm的红光。
   [G] = 光通量为 4.5907 lm的546.1 nm的绿光。
   [B] = 光通量为 0.0601 lm的435.8 nm的蓝光。

   这个公式表示的就是色彩的加色混合原理。

等能白光

当R、G、B系数都等于1时，可以混出equal energy white light （等能白光）。等能白光是光谱辐射密度在可见光范围内不变的一种光，这种光自然界中是不存在的，实验室可近似配制出来。标准白光的光通量可以表示为：1*1 + 1*4.5907 + 1*0.0601 = 5.6508 lm；此时，我们可称为，三基色光等量混合混为白光（这也是为什么 [R]、[G]、[B]代表光的光通量不同）。

注意equal energy white light （等能白光）和 白点（White Point）不一样。因为现实中不存在equal energy white light （等能白光）所以拿自然光中比较近似的比如D65作为白点（White Point）。

等能白光物理上的定义：

等能白光的定义是以辐射能作纵坐标、光谱波长为横坐标的光谱相对辐射能通量功率分布曲线是一条平行横轴的直线，即S（λ）=C（常数）。

2º 观察者

可能有很多人见过“2º 观察者” 这个名字，这是怎么回事？

其实，这个“2º 观察者” 就是从CIE 1931 RGB 来的。因为在当时的色彩匹配实验中，用户可以看到的视角只有2º。

2º 的视角是什么感觉? 假设有一张纸距离你 25 cm，在上面画一个半径 4.36mm 的圆圈，恩，这时候你的视角就是2º……

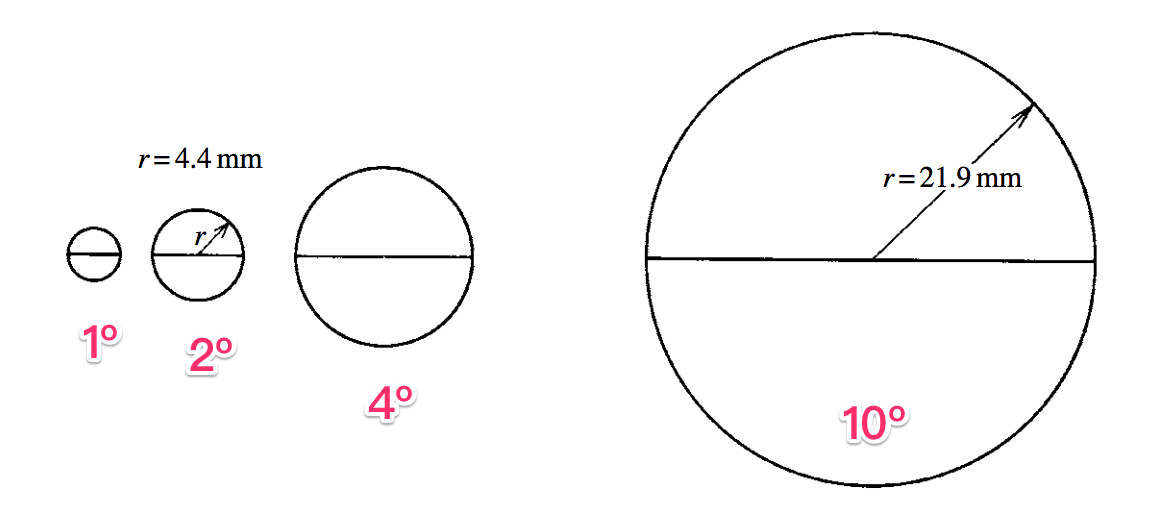
为什么看这么小的角度？CIE 当时有如下的考虑：

（1）视网膜上有个中心凹，这个地方有着最高的视觉分辨力，而这个中心凹对应的视角差不多是2º
（2）视网膜居中的区域有斑色素，如果超过4º 的视角，整个匹配结果就会有很大的变化

怎么样？听起来这两个理由是不是很有说服力？在一定程度上的确是非常好的考虑。

但是，还是那句话，色彩的感知还有很多生理上的特点。

例如，当你看到完全相同的两个颜色，只不过一个只是一个小圆点，另外一个是一整张A4 纸，你心理上的感觉会非常的不同。

再举个例子，装修刷墙的时候，你看到油漆小小的色卡，可能觉得某个颜色很适合，但是当这个颜色刷满一整面墙壁的时候，看起来的感觉可能会截然不同……（别问我怎么知道的！）

在这些条件的影响下，1959年，来自英国的Stiles和Burch，以及来自苏联的Speranskaya分别又做了色彩匹配实现，只不过这次，观看的视角变成了10º。

Stiles和Burch的实验有49个参与者，Speranskaya邀请了18 个测试者（之后涨到27人）。这些结果成为1964 CIE Standard Colorimetric System。在这个色彩系统中，观察者自然就叫做“10º 观察者”。

色彩匹配方程

CIE 很有耐心的把从380 nm ～ 780 nm波长中所有的光线都作为测试光，一个一个的重复上面的实验。
就得到了类似如下的数据：

380 nm ＝ 0 * [R] + 0 * [G] + 0.01 * [B]
381 nm = 0 * [R] + 0 * [G] + 0.02 * [B]
……
780 nm ＝ 0.01 * [R] + 0 * [G] + 0 * [B]

然后，我们把所有的数值都画在一张图表上面。就得到了三条曲线，这就是色彩匹配的信息。

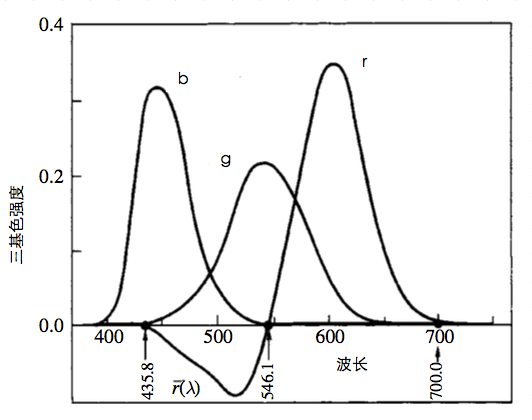
如果你很细心的观察，你会发现有从435.8 nm ～ 546.1 nm 这段波长中，红色基色的强度竟然是负值？！

难道还能出现吸收光亮的光线么？！

当然是不可能的，造成这个的原因是在这个波段中，测试者不论怎么努力的调整三基色的强度都无法让混合后的颜色与测试光源的颜色相同；最后只要在测试光源的那一侧混入一定量的红色才使得左右两边看起来颜色相同。

这个通过公式来说就是：

【测试光源】+ R * [R] ＝ G * [G] + B * [B]
（等式两遍同时减去 r * [R]）
【测试光源】 ＝ -R * [R] + G * [G] + B * [B]

这就是为什么出现了红色基色的强度出现了负值。

归一化

上面的色彩匹配方程其实已经完全足够了，但是科学家有个癖好，总是希望参数都是-1～1 之间的。这一步操作就叫做归一化。
归一化的计算也是异常的简单，原理就是算出每种基色强度在当前混色强度中所占的比例：

r = R / (R+G+B)
g = G / (R+G+B)
b = B / (R+G+B)

经过这样的计算之后，r、g、b 就都是在-1 ~ 1 之间了。而且很明显，我们发现 r + g + b = 1。

这么说的话，我们只需要知道r、g、b 三个参数中的任意两个，剩下的一个总是可以通过 1 - r - g 来得到。

也就是说，我们没有必要使用三个参数啦！只需要两个就够了！这也是归一化的另外一个优点。

图像化

这一步需要你稍微有点空间想象能力啦！

因为我们已经对数值进行归一化，因此只需要两个变量就足够表示所有的信息.

这里我们选择 r、g 这两个参数，那么b = 1 - r - g 是可以随时计算出来的。

所以我们画个图表，横坐标是r，纵坐标是g ，然后把所有的数值都画在这个图表上，就得到了。

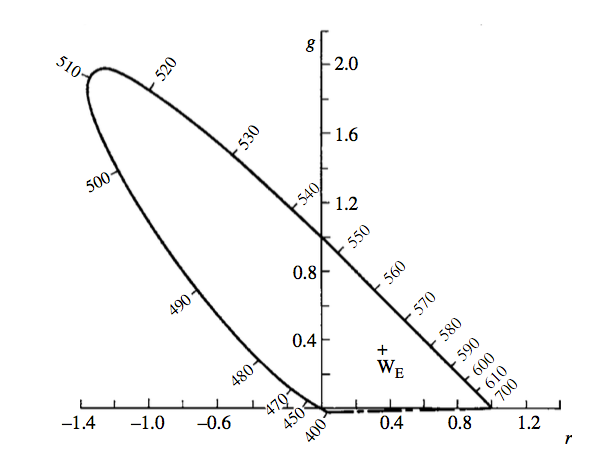
如果你仔细看看，会发现有很多波长的色彩都落在了 -r 的区域，还有一点点落在了 -g 的区域。

不管你懂不懂，总之只要你知道这是人类的色彩科学历史上第一次可以客观的来描述一个颜色！我们可以把任何一个可见光的颜色用这个图表中的一个点的坐标来表示。

当然这个RGB 色彩标准还有很多使用上的不便，之后科学家会通过各种方法来对他进行优化，来达到各式各样的目的：

（1）简化计算
（2）方便感知
（3）奇奇怪怪的需求

不过，对于后来所有的色彩空间、色彩标准，这个CIE 1931 RGB color specification system 绝对是色彩历史上的第一步！

一个小插曲：
CIE 1931 年观察者实验中的实验数据，其实只有 Guild 测试的7个人再上 Wright 测试的10个人……总共只有17个人。
现在动不动就大数据的年代，当时只有17个人…… 真是太简陋了。

CIE 1931 XYZ Color Specification System【1931】

言归正传，CIE 1931 RGB 色彩系统看起来已经挺不错的了，但是他有一个很大的问题那就是存在负数！

虽然这个问题不会造成错误，但是对于实现计算来说就很麻烦。

试想一下，如果每次计算的时候都需要判断一下输入的是正数还是负数，就非常浪费时间了。

于是，人们就希望有一个新的色彩空间，可以满足以下的一些特性：

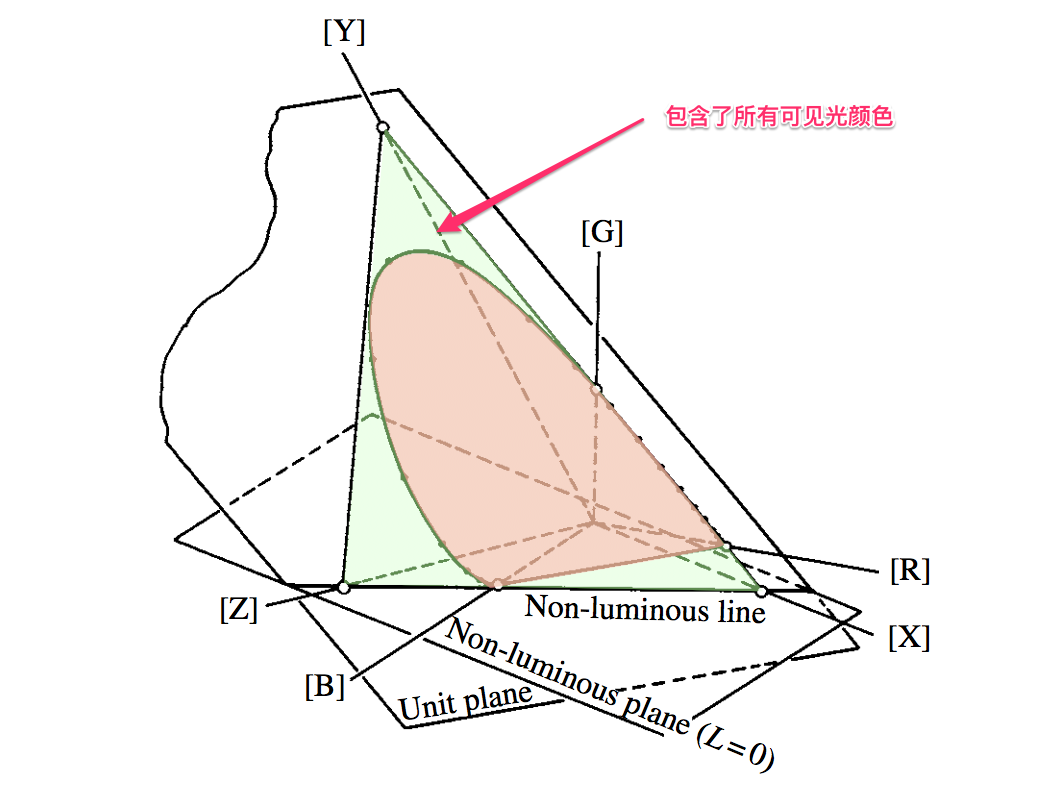
（1）包含所有人眼可见光
（2）所有 XYZ 数值都是正数，方便计算
（3）三个色彩分量中的Y，可以直接表示光的亮度
（4）如果光的波长 ≥ 650 nm，可以直接让 Z 分量 = 0，进一步简化计算

这里不讨论具体的细节，但是需要强调一下XYZ 色彩空间的意义。

首先，XYZ 色彩空间不是实验得到的，他是在CIE 1931 RGB 色彩系统的基础上，通过数学的手段得到的。

XYZ 色彩空间的目的主要就是为了简化计算，所以XYZ 可以说是一个非常好的“中转” 色彩空间。

比方说，如果你想从 A 空间 变成 B 空间，那么推荐的方式是实现 A 到 XYZ，再实现 XYZ 到B。

看起来浪费了一步，等色彩空间复杂起来之后，这种方式优势就大多了！

说了那么多，如果想要直接知道结论，这里就是：任何色彩空间的变换都可以理解为三维空间变换，所以只需要3x3 的矩阵就可以表示出来：

这里的RGB 是CIE 1931 RGB，可不是sRGB 里面的RGB 数值哦！

如果你有兴趣了解从CIE 1931 RGB 到 XYZ 的过程，可以看看线性代数哦……

归一化

当你有了三个变量，你想要用两个变量来表示……怎么办？
没错！ 又是归一化！

和 R、G 变成r、g 两个变量相同， 把XYZ 三个变量，变成x、y 两个变量，相当于求得了每个分量在总体中所占的比重：

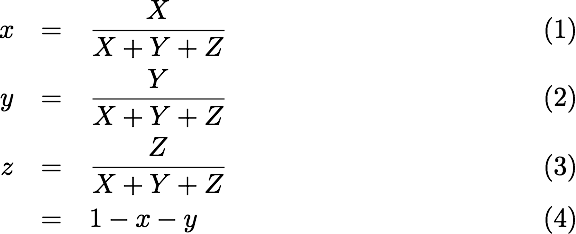
这时候，我们选择x、y 作为平面坐标系的两个轴，那么人眼所有可见的色彩范围是什么样子？

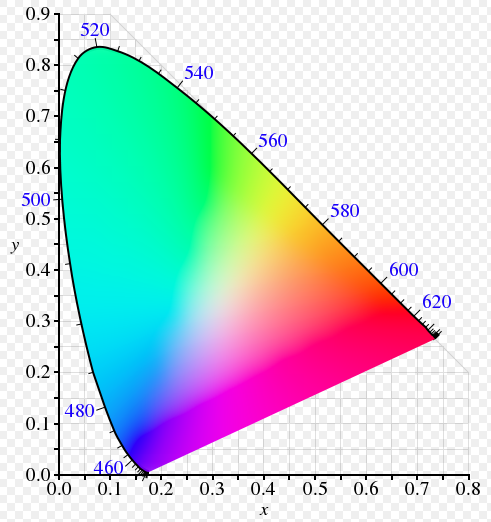
怎么样？是不是很熟悉？

没错，这就是传说中的人眼可见光范围的表示。

如果有细心的读者，没准可以发现，从这个图像上虽然可以分辨出所有的颜色，但是好像没有了亮度的区别？

比方说，有一个光线c = (0.612, 0.256)，我增强光线的强度或者降低光线的强度，人眼看到的颜色肯定不同，但是从 xy 来看，得到的坐标总是相同的……

没错，由于二维坐标 xy 只可能表示一个平面，那么亮度怎么办？

于是乎，在归一化 xy 的基础上，科学家们又把 XYZ 中的 Y 单独拿出来，与 xy 一起，组成了xyY 色彩空间。其中：

（1）xy 表示色度，x、y代表CIE1931—RGB标准色度观察者光谱三刺激值色度图上的x坐标、y坐标
（2）Y 表示亮度

这样就搞定了！

什么是 Yxy？对不起这里有点超纲啦……

总结

XYZ 色彩空间知道现在依然是极其重要的色彩标准之一。
当你需要计算色彩空间转换之类的时候，基本上一定会用到XYZ。

W*U*V 和 L*a*b 和 L*u*v* 【1964 - 1976】

别看花了眼睛，这里是三个色彩空间：

W*U*V*
L*a*b*
L*u*v*

怎么这次一口气来了三个色彩空间？因为它们三个有类似的特性。

有人可能会说，刚刚还在说XYZ 色彩空间如何如何好，怎么现在有需要的新的色彩空间了？

XYZ色彩空间的缺憾

没错，XYZ 色彩空间包含了所有可见光、计算简便、适合做“中转” 色彩空间，但是他有一个缺憾：色彩分布不是均匀的。

这要怎么理解？我们来举个例子：想象有一张地图，你家住在A 点，你公司在B 点。AB 之间的直线距离是d，完美情况下（你可以穿墙、走直线距离、没有红绿灯……）你需要T 分钟走到公司。有一天你搬家了，搬到了C 点，新的公司在D。凑巧的是CD 之间的距离也是d，那么完美情况下，你也只需要T 分钟走到公司。这很符合常识，没有问题。

我们回到上一节的 xy 色度坐标。我有一个颜色A，和另一个颜色B。AB 之间的距离是d，看起来的颜色差异是T。我们选择另外一组颜色C和颜色D，CD 之间的距离也是d，那么色彩看起来的差异也应该是T，对吧？很可惜，答案是NO。

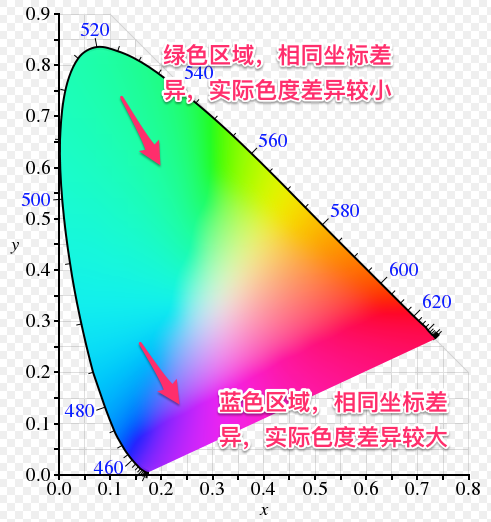
比方说，我用相同长度的箭头表示在xy 色度坐标下的距离，可以明显看出，绿色区域内的箭头两端看起来差异比较小，而蓝色区域的差距就很大。

这就造成一个问题，我很难通过只计算两个颜色的之间的距离，就能够直观的感受到两个颜色之间的差异有多大。

uniform 类型的色彩空间

为了解决这个问题，就出现了一类叫做uniform colorspace的色彩空间。【人欲无穷啊……】

“看起来差异差不多” 这件事情是一个主观的判断，当色彩科学中一遇到主观问题的时候，我们就需要“做实验”！

Wright 在1941年给出了一组数据，在相同的照明情况下，不同颜色可以分辨出的细小不同。

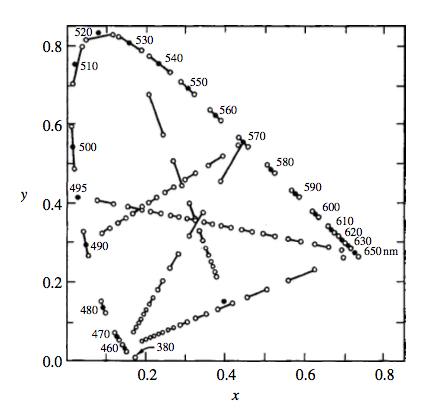
这些小短线表示的是可以发觉出颜色不同的距离。

线段长，表示颜色在坐标数值上需要变化很多，人眼才能发现不同。
线段短，表示只需要变化很小的坐标，人眼就会发觉颜色不同。

后来，Wright和Pitt一起对单波长的光线进行了这种测试，调整不同波长光线的强度，直到人眼“将将可以分辨”出区别（JND, just-noticeable difference）。

后来1942年，David Lewis MacAdam又做了一个更详细的实验。和Wright只在某个方向上测量将将可以分辨出色彩差异的坐标距离不同，MacAdam测量了一个范围，这个范围内的颜色都是人眼发觉不出区别的。

于是乎，上面图像中的线段，就变成了下面这个图片中的一个个椭圆：

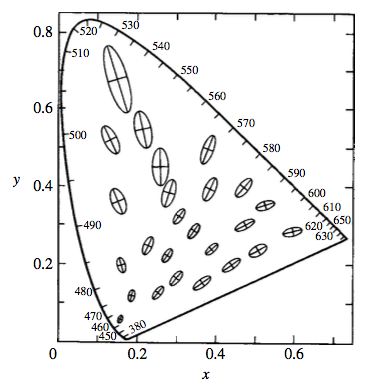
我们的最终目的就是希望有个新的色彩空间，是“均匀分布”的。

换句话说，就是通过某种变形，让上面图片中的椭圆，都变得差不多大。

这样就保证了坐标距离相同的情况下，色彩的差异性也是相同的。

于是CIE 在1960年使用了MacAdam的转换方程，将xy 色度坐标，转换为uv 色度坐标：

通过这样的变换，xy 色度坐标内的那些椭圆就变成了下面的样子（虽然不对，但是可以试着这样理解一下，把上面xy 色度坐标上下挤压一下，左右拉伸一下，最后再非均匀的从下方往上方周围推推，好像橡皮泥一样）：

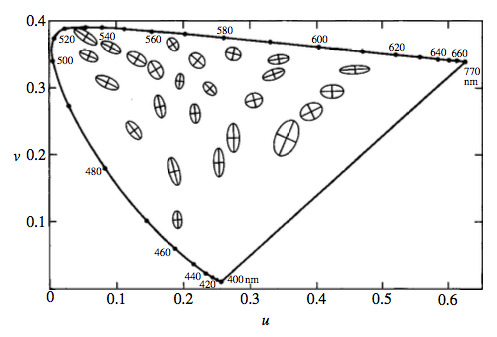
怎么样，是不是现在看起来就均匀多了？

现在色度的均匀解决了，接下来就是亮度了。Yxy中的 Y 所表示的亮度也存在非均匀的问题，因此还需要对亮度进行处理。

Wyszecki在CIE 1960 uv 色度坐标的基础上提出了下面的W*U*V* 色彩空间：

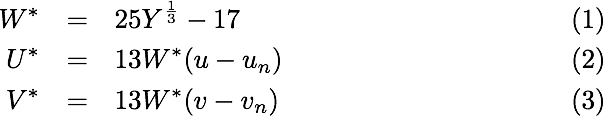
这就是CIE 1964 W*U*V* 色彩空间。

这个色彩空间现在的人知道的应该不是很多了，因为在1976年，CIE 推荐使用两个新的色彩空间，这两个色彩空间就是 L*a*b* 和 L*u*v。相信这两个色彩空间知道的人就多很多了，不过注意，上面都是有*号的哦！要专业！

这里不会再进一步列举每个色彩空间的公式了（有兴趣可以去搜索维基百科，里面的解释很详细）。

对于读者来说更重要的是知道L*a*b* 和 L*u*v*这两个色彩空间，L* 都是对亮度进行了uniform 处理，同时色度坐标也是uniform 的。

回忆一下上面关于地图上家到公司之间的距离那个例子，现在在这种均匀的色彩空间内，两个颜色坐标之间的距离（欧氏距离），就可以代表人眼看到他们实际上相差的有多大了！假设AB 两个颜色之间的距离为0.2，另外两个颜色CD 之间的距离是0.47，你就可以非常有信心的说：“CD 看起来的差异比AB 要大！”

总结

这一节说的内容有点多…… 也有点枯燥……

但是一定要知道XYZ 色彩空间直到现在依然是极其重要的色彩标准之一，当你需要计算色彩空间转换之类的时候，基本上一定会用到 XYZ。

而L*a*b* 和 L*u*v*这两个色彩空间 也是目前最常用的uniform 类型的色彩空间，在反应实际色彩感知的时候，这种均匀的色彩空间会帮你更多~

参考文档

第一章 我们为什么能感觉到颜色？
第二章 色彩空间的历史书
流明和坎德拉的關係
以眼睛的名义：一些光度学概念的解析